La ecuación de onda es una expresión matemática cuyas soluciones describen el movimiento de muchas clases de onda. Las ondas son perturbaciones en el espacio y en el tiempo, así que su representación matemática es una función que depende de la posición y el instante de observación.
Como primer ejemplo, uno de los casos más simple de onda es la que se forma a lo largo de una cuerda tensa, en la cual la onda se distribuye a lo largo de la cuerda. La posición longitudinal de un punto de la cuerda se denota con “x”, mientras que el instante de tiempo en el que se observa se denota mediante “t”.
Cuando la cuerda está tensa y sin perturbar, la posición transversal de cada punto x de la cuerda es y = 0. Pero al ser perturbada, la coordenada transversal toma diferentes valores en cada punto y en cada instante, por lo que la posición transversal pasa a ser una función de “x” y “t”:
\(y = f (x, t)\)
La ecuación que describe la evolución de la perturbación en el espacio y en el tiempo es una ecuación diferencial de segundo orden en las derivadas espaciales y temporales, de allí que las derivadas sean derivadas parciales. Se denomina “ecuación de onda” y toma la forma:
\(\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}}=\left( {\frac{1}{{{{v}^{2}}}}} \right)~\frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
El parámetro “v” es la velocidad de propagación de la onda a lo largo de la cuerda, y la solución de la ecuación, la función y (x, t), se conoce como función de onda.
Fórmulas para la deducción matemática de la ecuación de onda
La ecuación de onda se deduce fácilmente a partir de la segunda ley de Newton, la cual vincula la fuerza neta con la aceleración.
Se derivará la ecuación de onda unidimensional que describe el movimiento vertical en una cuerda por la que viaja una onda, pero este modelo también se puede aplicar a los cambios de presión en una onda sonora, o a una onda electromagnética.
Para encontrar la ecuación, se utiliza un pequeño segmento de la cuerda, como el que se muestra en la figura. La onda es transversal, de manera que la oscilación de las partículas en la cuerda ocurre en el eje vertical.
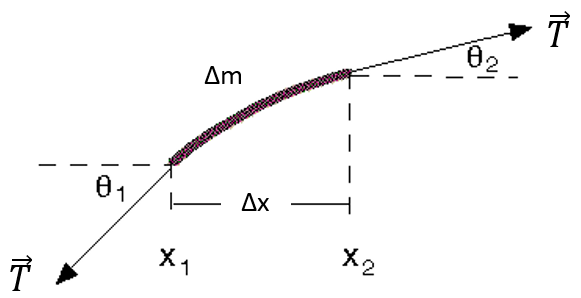
Los extremos del segmento están sujetos a la misma tensión \(\vec{T}\), y para deducir la ecuación, se parte de que la amplitud de la onda es pequeña.
Fórmulas para la aproximación del ángulo pequeño
Si la amplitud de la onda es pequeña, los ángulos θ1 y θ2 también. Esta suposición facilita el análisis, porque cuando un ángulo es pequeño, ocurre que:
\(sen~\text{ }\!\!\theta\!\!\text{ }\approx \tan \theta \)
Y:
\(\cos \theta \approx 1\)
Esto se conoce como “aproximación del ángulo pequeño”.
Dado que la derivada es la pendiente de la recta tangente a la curva en un cierto punto, y esta pendiente equivale a la tangente del ángulo de inclinación, también se tiene que:
\(sen~\text{ }\!\!\theta\!\!\text{ }\approx \tan \theta =\frac{{\partial y}}{{\partial x}}\)
Fórmulas de la segunda ley de Newton
El siguiente paso es aplicar la segunda ley de Newton al segmento de cuerda, cuya masa es Δm. Es conveniente expresar esta masa en términos de la densidad lineal de masa de la cuerda (masa por unidad de longitud), llamada μ. De esta manera:
Con esto en mente, se aplica la segunda ley de Newton y la aproximación del ángulo pequeño:
\(\sum {{F}_{x}}=~T\cdot cos{{\theta }_{2}}-T\cdot cos{{\theta }_{1}}=0\)
En cuanto a las fuerzas sobre el eje vertical:
\(\sum {{F}_{y}}=~T\cdot sen{{\theta }_{2}}-T\cdot sen{{\theta }_{1}}=\mu \text{ }\!\!\Delta\!\!\text{ }x\cdot {{a}_{y}}\)
Donde \({{a}_{y}}\) es la aceleración, que también es la segunda derivada de la posición con respecto al tiempo:
\({{a}_{y}}=\frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
Sustituyendo en la segunda ley de Newton:
\(T\left( {sen{{\theta }_{2}}-sen{{\theta }_{1}}} \right)=\mu \text{ }\!\!\Delta\!\!\text{ }x\cdot \frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
Continuando con la aproximación del ángulo pequeño:
\(T\left( {\tan {{\theta }_{2}}-\tan {{\theta }_{1}}} \right)=\mu \text{ }\!\!\Delta\!\!\text{ }x\cdot \frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
\(T\left( {\frac{{\partial {{y}_{2}}}}{{\partial x}}-\frac{{\partial {{y}_{1}}}}{{\partial x}}} \right)=\mu \text{ }\!\!\Delta\!\!\text{ }x\cdot \frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
Ahora se divide todo por Δx:
\(T\left[ {\frac{{\left( {\frac{{\partial {{y}_{2}}}}{{\partial x}}-\frac{{\partial {{y}_{1}}}}{{\partial x}}} \right)}}{{\text{ }\!\!\Delta\!\!\text{ }x}}} \right]=\mu \cdot \frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
Tomando el límite en el lado izquierdo, cuando Δx → 0, se obtiene por definición la derivada (parcial) respecto de “x”, de la derivada de “y” respecto de “x”. Es decir, la segunda derivada parcial de “y” con respecto a “x”:
Sustituyendo este resultado en la expresión anterior:
\(\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}}=\frac{\mu }{T}\cdot \frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
Por último, se sabe que la velocidad “v” de la onda en la cuerda viene dada por:
\(v=\sqrt{{\frac{T}{\mu }}}\)
Ya que en general, la velocidad de una onda viene dada por:
\(v=\sqrt{{\frac{{Propiedad~restauradora}}{{Propiedad~inercial}}}}\)
En este caso, la propiedad restauradora pertenece a la tensión, mientras que la inercial es la densidad de masa.
Al sustituir esta fórmula para la velocidad, se obtiene finalmente la ecuación de onda descrita al comienzo:
\(\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}}=\left( {\frac{1}{{{{v}^{2}}}}} \right)~\frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
Solución de la ecuación de onda
Una vez que se tiene la ecuación de onda, que es una ecuación diferencial en derivadas parciales, ya que las dos variables: “x” y “t” se encuentran dentro de las derivadas, el próximo paso es encontrar su solución.
Es fácil demostrar, llevando a cabo las derivadas necesarias, que la solución tiene la forma:
\(f\left( {x\pm vt} \right)\)
Asimismo, la superposición de dos soluciones a \({{f}_{1}}+b{{f}_{2}}\), con a y b constantes, también la satisface. Entonces, ¿cuál solución elegir?
Generalmente para f1 y f2 se eligen las funciones trigonométricas seno y coseno. A estas funciones se les conoce como “funciones armónicas” y brindan soluciones apropiadas y convenientes a la ecuación de onda.
Ello se debe a que cualquier onda de forma arbitraria, se puede representar como una superposición de funciones seno y coseno, con frecuencias múltiplos de la frecuencia fundamental. Este es el conocido teorema de Fourier.
Ejemplo práctico
Mostrar que la función:
\(y=sen~x\cdot \cos \left( {vt} \right)\)
Es una solución de la ecuación de onda.
Respuesta
Hay que realizar las derivadas indicadas en la ecuación y sustituirlas en esta, para verificar que la igualdad se cumple. Si se cumple, la función dada es, en efecto, solución de la ecuación.
Las derivadas parciales se llevan a cabo de la misma manera que las derivadas ordinarias, suponiendo que la otra variable se mantiene constante.
\(\frac{{\partial y}}{{\partial x}}=\frac{\partial }{{\partial x}}\left[ {sen~x\cdot \cos \left( {vt} \right)} \right]=cos~x\cdot \cos \left( {vt} \right)\)
\(\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}}=\frac{\partial }{{\partial x}}\left[ {cos~x\cdot \cos \left( {vt} \right)} \right]=-sen~x\cdot \cos \left( {vt} \right)\)
\(\frac{{\partial y}}{{\partial t}}=\frac{\partial }{{\partial t}}\left[ {sen~x\cdot \cos \left( {vt} \right)} \right]=sen~x\cdot \left[ {-v\cdot \text{sen}\left( {vt} \right)} \right]\)
\(\frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}=\frac{\partial }{{\partial t}}\left\{ {sen~x\cdot \left[ {-v\cdot \text{sen}\left( {vt} \right)} \right]} \right\}=-{{v}^{2}}\cdot sen~x\cdot \cos \left( {vt} \right)\)
Solo las segundas derivadas se sustituyen en la ecuación de onda:
\(\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}}=\left( {\frac{1}{{{{v}^{2}}}}} \right)~\frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}\)
\(-sen~x\cdot \cos \left( {vt} \right)=\left( {\frac{1}{{{{v}^{2}}}}} \right)~\left[ {-{{v}^{2}}\cdot sen~x\cdot \cos \left( {vt} \right)} \right]\)
Puesto que el signo negativo y el cuadrado de la velocidad se cancelan, se obtiene la igualdad buscada:
\(sen~x\cdot \cos \left( {vt} \right)=sen~x\cdot \cos \left( {vt} \right)~\)
Por lo tanto, se concluye que la función propuesta es una solución de la ecuación de onda.
Referencias bibliográficas
Figueroa, D. Física para Ciencias e Ingeniería: Ondas y Física Cuántica. Volumen 7. Editado por D. Figueroa, PhD.Giancoli, D. Física para Ciencias e Ingeniería. Volumen 1. 4ta. Edición. Prentice Hall.
