La fuerza de Lorentz describe la dinámica de una carga eléctrica q, que se mueve bajo la acción de un campo electromagnético con una velocidad \(\vec{v}\) . Si \(\vec{E}\) es el campo eléctrico y \(\vec{B}\) es el campo magnético, la fuerza de Lorentz \({{\vec{F}}_{L}}\) tiene la forma:
\(~{{\vec{F}}_{L}}={{\vec{F}}_{E}}+{{\vec{F}}_{M}}=q\vec{E}+q\vec{v}\times \vec{B}\)
De esta forma, la fuerza de Lorentz toma en cuenta la contribución del campo eléctrico \({{\vec{F}}_{E}}\) así como la del campo magnético \({{\vec{F}}_{M}}\), sobre el movimiento de la partícula cargada.
El nombre de la ecuación se debe al físico holandés Hendrik Anton Lorentz (1853-1928), quien realizó extensas contribuciones en el campo de la física teórica, sentando las bases que sirvieron para que Einstein desarrollara posteriormente su teoría de la relatividad.
Al usar la ecuación de la fuerza de Lorentz, los campos y el movimiento de la partícula cargada se observan todos desde el mismo marco de referencia. Ahora bien, si la velocidad de la carga es 0, entonces la fuerza de Lorentz se reduce a:
\({{\vec{F}}_{L}}=q\vec{E}\)
Ello se debe a que la partícula cargada solo experimenta fuerza magnética cuando está en movimiento, y su velocidad no es paralela al campo magnético.
Ejemplos de aplicación de la Fuerza de Lorentz
El selector de velocidades
Supóngase que se tiene un haz de partículas cargadas, formado por iones. Cada partícula se mueve a determinada velocidad en el campo electromagnético, por lo que una manera de identificar a la partícula es hacer que viaje a una velocidad determinada.
Esto es posible si se configuran los campos eléctrico y magnético a través de los cuales se mueven los iones, de tal forma que sean perpendiculares entre sí y también a la velocidad de la partícula. A esta configuración se le conoce como “campos cruzados”.
Si una partícula de masa m y carga q positiva, se mueve en campos cruzados, se ajusta la intensidad de estos para que las respectivas fuerzas se opongan, lo que da como resultado que la fuerza de Lorentz se anule.
De esta forma, el ión se mueve en línea recta con una determinada velocidad constante.
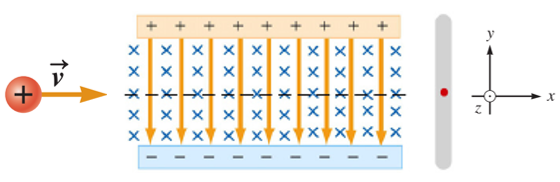
En la figura de arriba está el esquema del selector. A la izquierda se observa un ión positivo, moviéndose con velocidad horizontal hacia la región donde están los campos cruzados. El sistema de coordenadas cartesianas para indicar la dirección de los vectores está a la derecha; la dirección +z apunta hacia fuera de la pantalla, simbolizada por el puntito encerrado en el círculo.
El campo eléctrico \(\vec{E}\) uniforme se genera por las dos placas cargadas y está dirigido verticalmente hacia abajo (flecha anaranjada). Por su parte, el campo magnético \(\vec{B}\), también uniforme, se genera entre los polos de un electroimán, que no aparece en el dibujo. El campo magnético se dirige hacia dentro de la pantalla, lo que se simboliza con la ×.
Sobre la partícula, el campo \(\vec{E}\), ejerce una fuerza en −y (hacia abajo), pues la placa con carga positiva la repele. La fuerza ejercida por el campo magnético se obtiene a través de \({{\vec{F}}_{M}}=q\vec{v}\times \vec{B}\). Siendo un producto vectorial, se aplica la regla de la mano derecha para determinar la dirección de la fuerza magnética, como sigue:
• Colocar el dedo índice apuntando hacia el eje +x, que es la dirección de la velocidad.
• El dedo medio debe apuntar hacia dentro de la pantalla o la hoja de papel, que es la dirección del campo magnético.
• El pulgar da la dirección y el sentido de la fuerza magnética, que en este caso es hacia arriba, en +y.
Dado que las fuerzas eléctrica y magnética tienen la misma dirección y sentido contrario, se anulan cuando sus magnitudes son iguales:
\(qE=qvB\)
Ya que la carga se cancela, el ión se mueve con rapidez igual a:
\(v=\frac{E}{B}\)
Las partículas que tengan esa velocidad inciden en el punto rojo de la pantalla que está a la salida de los campos cruzados, y así son seleccionadas. El ejemplo muestra una partícula positiva, pero el selector funciona igualmente con iones negativos o con electrones.
El espectrómetro de masas
Es un instrumento utilizado en el análisis químico de las sustancias, mediante el cual se puede conocer su composición molecular. Los primeros espectrómetros de masas fueron construidos por Francis Aston (1877-1945) en 1919. Aston era discípulo de J.J. Thomson (1856-1940), el físico inglés que, valiéndose de esta técnica, descubrió el electrón el 30 de abril de 1897.
Para conocer la composición de una sustancia, se ioniza una muestra mediante una diferencia de potencial elevada. De esta forma, la molécula se fragmenta en iones y seguidamente, el haz de partículas formado se proyecta hacia el selector de velocidades.
Los campos del selector se fijan para escoger solo las partículas que tengan una cierta velocidad, bloqueando a todas las demás. Seguidamente, se hace ingresar el haz seleccionado en una región donde solo existe campo magnético.
Cuando una partícula cargada entra perpendicularmente a una región de campo magnético uniforme, se desvía de tal manera que su movimiento se transforma en un movimiento circular uniforme (MCU). La fuerza magnética es la encargada de proporcionar la aceleración centrípeta:
\({{\vec{F}}_{M}}=m\cdot {{\vec{a}}_{c}}\)
La magnitud de la aceleración es:
\({{a}_{c}}=\frac{{{{v}^{2}}}}{R}\)
Donde v es la rapidez y R es el radio de la trayectoria circular. Sustituyendo la fuerza magnética y la aceleración centrípeta, se obtiene esta ecuación:
\(qvB=m\left( {\frac{{{{v}^{2}}}}{R}} \right)\)
Y ahora, se despeja la razón masa-carga:
\(\frac{m}{q}=\frac{{vRB}}{{{{v}^{2}}}}=\frac{{RB}}{v}\)
La relación masa-carga de la partícula depende del radio de la trayectoria R, la magnitud del campo magnético B y la rapidez v que tenía al salir del selector.
Con esta técnica, al modular el cociente E/B, se compone un espectro de relaciones masa–carga para los iones presentes en la muestra de sustancia.
Un espectro de relaciones masa-carga tiene la forma de señales verticales como las que se muestran en la siguiente figura. La molécula analizada allí es la del diisopropil éter, un compuesto que suele utilizarse como solvente.
En el eje vertical se grafica la abundancia de iones, mientras que en el eje horizontal está la relación masa-carga. Cada fragmento de la molécula tiene una de estas señales, que indica la masa molar del fragmento, por lo tanto, analizando el espectro y las cantidades presentes, se puede conocer la composición de la molécula.
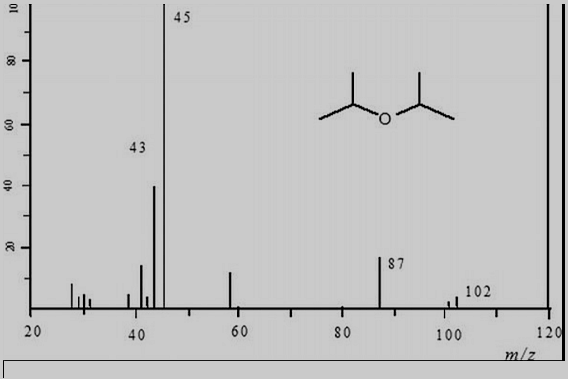
Imagen de la Facultad de Química de la UNAM.
