En el año 1785 el físico, matemático e ingeniero francés, Charles Coulomb, estableció la ley fundamental de la fuerza eléctrica, que permite determinar la acción a distancia que existe entre cargas eléctricas.
La electrificación de los cuerpos se manifiesta a través de la existencia de fuerzas electrostáticas ejercidas entre los cuerpos electrificados. Estas fuerzas pueden ser, dependiendo de la naturaleza de la carga de los cuerpos que interactúan, de atracción (entre cuerpos de cargas con signos diferentes) o de repulsión (entre cuerpos de cargas de signos iguales). Así, la electrostática es construida a partir de la Ley de Coulomb.
Propiedades de la Ley de Coulomb
Coulomb, a través de una serie de experimentos realizados utilizando una balanza de torsión, que él mismo inventó en el año 1977, demostró que la fuerza eléctrica dada en presencia de dos partículas cargadas o cargas puntuales \({{Q}_{1}}\) y \({{Q}_{2}}\) , separadas una distancia \(r\) , como las mostradas en la figura 1, posee las siguientes propiedades:
• “La fuerza eléctrica es directamente proporcional al producto de las magnitudes de las dos cargas puntuales \({{Q}_{1}}\) y \({{Q}_{2}}\).”
• “La fuerza eléctrica es inversamente proporcional al cuadrado de la distancia \(r\) que separa las cargas y se encuentra dirigida a lo largo de la línea que une a las dos cargas puntuales \({{Q}_{1}}\) y \({{Q}_{2}}\).”
• “La fuerza eléctrica es de atracción si las dos cargas puntuales \({{Q}_{1}}\) y \({{Q}_{2}}\) tienen signos diferentes, o de repulsión si tiene signos iguales.”
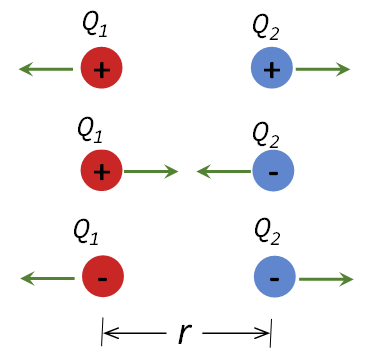
Figura 1. Fuerza eléctrica entre dos partículas cargadas.
Para expresar matemáticamente estos resultados, Coulomb introdujo una constante de proporcionalidad \({{k}_{C}}\), conocida como constante de Coulomb. Esta constante depende del medio en el cual se encuentren las cargas; cuando este medio es el vacío o espacio libre, tiene un valor de \(8.9875~\times ~{{10}^{9}}~{}^{N\cdot {{m}^{2}}}\!\!\diagup\!\!{}_{C}\;\). La constante de Coulomb se puede expresar en función de la constante de permitividad del espacio libre ( \({{\varepsilon }_{0}}\) ) como:
\({{k}_{C}}~=~\frac{1}{4\pi {{\varepsilon }_{0}}}\)
Donde \({{\varepsilon }_{0}}~=8.8542~\times ~{{10}^{-12}}~{}^{C}\!\!\diagup\!\!{}_{N\cdot {{m}^{2}}}\;\)
Para simplificar los cálculos se suele utilizar el valor de \(9~\times ~{{10}^{9}}~{}^{N\cdot {{m}^{2}}}\!\!\diagup\!\!{}_{C}\;\), como constante de Coulomb en el vacío o espacio libre.
De esta forma, la expresión matemáticas de la Ley de Coulomb para calcular la magnitud de la fuerza eléctrica entre las dos cargas puntuales representadas en la figura 1, se escribe como:
\(F~=~{{k}_{C}}~\frac{\left| {{Q}_{1}} \right|~\left| {{Q}_{2}} \right|}{{{r}^{2}}}\) ó \(F~=~\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{\left| {{Q}_{1}} \right|~\left| {{Q}_{2}} \right|}{{{r}^{2}}}\)
La unidad de la carga eléctrica en el sistema internacional de unidades (SI) es el Coulomb (C). En la naturaleza, la unidad de carga más pequeña que se conoce es la carga del electrón o del protón, cuya magnitud es igual a \(1.60219~\times {{10}^{-19}}~\)C.
La fuerza eléctrica obedece a la tercera ley de Newton, es decir, que la fuerza que \({{Q}_{1}}\) ejerce sobre \({{Q}_{2}}\) es de igual magnitud, pero sentido contrario, a la fuerza que \({{Q}_{2}}\) ejerce sobre \({{Q}_{1}}\).
En la figura 2, \({{\vec{F}}_{12}}\) representa la fuerza que \({{Q}_{2}}\) ejerce sobre \({{Q}_{1}}\)., mientras que \({{\vec{F}}_{21}}\) representa la fuerza que \({{Q}_{1}}\) ejerce sobre \({{Q}_{2}}\).
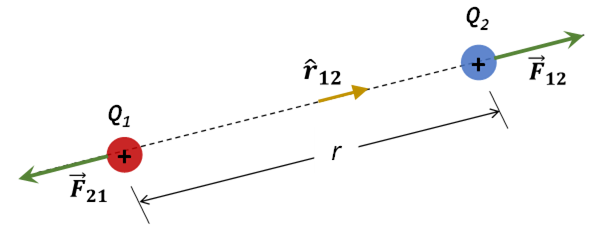
Figura 2. Representación de la fuerza eléctrica entre dos cargas puntuales.
La fuerza eléctrica que \({{Q}_{1}}\) ejerce sobre \({{Q}_{2}}\) la podemos expresar de forma vectorial como:
\({{\vec{F}}_{12}}~=~{{k}_{C}}~\frac{\left| {{Q}_{1}} \right|~\left| {{Q}_{2}} \right|}{{{r}_{12}}^{2}}~{{\hat{r}}_{12}}\)
Donde \({{\hat{r}}_{12}}\) es el vector unitario dirigido de \({{Q}_{1}}\) a \({{Q}_{2}}\), es decir, desde quien ejerce la fuerza hacia quien la recibe.
Cuando en lugar de dos cargas puntuales tenemos un sistema constituido por n cargas puntuales, la fuerza eléctrica resultante sobre cualquiera de ellas es igual a la suma algebraica de cada uno de los vectores fuerza que las demás cargas ejercen sobre ella. Esto es lo que se conoce como principio de superposición.
Ejemplo práctico
Considere el sistema de tres cargas puntuales ubicadas en los vértices de un triángulo equilátero de lados 6 cm, mostrado en la figura 3. Determine la fuerza eléctrica que actúa sobre \({{Q}_{1}}\).
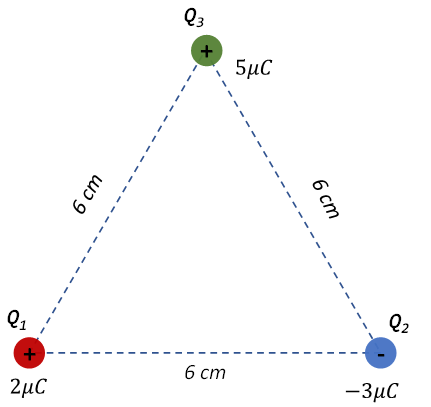
Figura 3. Sistema de cargas puntuales.
Para determinar la fuerza eléctrica sobre \({{Q}_{1}}\), lo primero es fijar un sistema de referencia (sistema cartesiano), cuyo origen, por conveniencia, ubicaremos en \({{Q}_{1}}\). Luego realizaremos el diagrama de cuerpo libre (DCL), dibujando los vectores fuerza que actúan sobre dicha carga (figura 4).
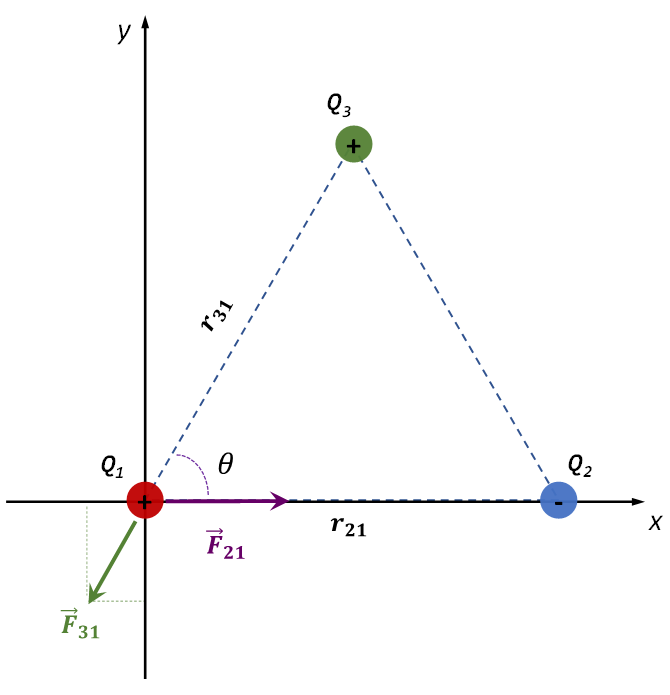
Figura 4. Diagrama de cuerpo libre del sistema de cargas puntuales.
Al aplicar el principio de superposición, la fuerza eléctrica total que actúa sobre \({{Q}_{1}}\) seria:
\({{\vec{F}}_{1T}}~={{\vec{F}}_{21}}~+~~{{\vec{F}}_{31}}~=~{{F}_{21}}~{{\hat{r}}_{21}}~+~{{F}_{31}}~{{\hat{r}}_{31}}\)
Puesto que \({{Q}_{1}}\) y \({{Q}_{2}}\) son cargas de signos diferentes, \({{Q}_{2}}\) ejercerá un efecto de atracción sobre \({{Q}_{1}}\), mientras que \({{Q}_{3}}\) ejercerá sobre \({{Q}_{1}}\) un efecto de repulsión, ya que ambas cargas son positivas.
Como podemos apreciar en la figura 4, el vector \({{\vec{F}}_{21}}\) sólo posee una componente horizontal, mientras que \({{\vec{F}}_{31}}\) es un vector ubicado en el tercer cuadrante, cuyas componentes \(x,~y\) se pueden determinar en función del ángulo \(\theta \) . Por lo tanto, los vectores \({{\vec{F}}_{21}}~~\)y \(~{{\vec{F}}_{31}}\) se escriben en función de sus componentes \(x,~y\), de la forma:
\({{\vec{F}}_{21}}~~=~{{F}_{21}}~\hat{i}~~\)
\({{\vec{F}}_{31}}~~=~-{{F}_{31}}\cos \theta ~\hat{i}-{{F}_{31}}\text{sen}\theta ~\hat{j}\)
Por tratarse de un triángulo equilátero, \(\theta ~=60{}^\circ \).
Ahora aplicamos la Ley de Coulomb para calcular la magnitud de \({{\vec{F}}_{21}}~~\)y \(~{{\vec{F}}_{31}}\):
\({{F}_{21}}~={{k}_{c}}\frac{{{Q}_{1}}~{{Q}_{2}}~}{r_{21}^{2}}~~\) y \({{F}_{31}}~=~~{{k}_{c}}\frac{{{Q}_{1}}~{{Q}_{3}}~}{r_{31}^{2}}\)
Antes de sustituir los valores de carga y distancia, debemos expresarlos en las unidades fundamentales del SI, es decir, la carga en coulomb y la distancia en metros, así:
\({{Q}_{1}}~=2\mu C~=2~\times ~{{10}^{-6}}~C\)
\({{Q}_{2}}~=-3\mu C~=-3\times ~{{10}^{-6}}~C~\)
\({{Q}_{3}}~=5\mu C~=~\)5 \(\times ~{{10}^{-6}}~C\)
\({{r}_{21}}~={{r}_{31}}~=~6~cm~=~6\text{ }\!\!~\!\!\text{ }\times ~{{10}^{-2}}~m\)
Finalmente, sustituyendo en la ecuación de fuerza total:
\({{\vec{F}}_{1T}}~={{k}_{c}}\frac{{{Q}_{1}}~{{Q}_{2}}~}{r_{21}^{2}}~\hat{i}~+{{k}_{c}}\frac{{{Q}_{1}}~{{Q}_{3}}~}{r_{31}^{2}}~\left( -\cos \theta ~\hat{i}-\text{sen}\theta ~\hat{j} \right)\)
Agrupando términos semejantes:
\({{\vec{F}}_{1T}}~={{k}_{c}}{{Q}_{1}}\left[ ~\left( \frac{~{{Q}_{2}}~}{r_{21}^{2}}-\frac{{{Q}_{3}}~}{r_{31}^{2}}~\cos \theta ~ \right)~\hat{i}-\frac{~{{Q}_{3}}~}{r_{31}^{2}}~\text{sen}\theta ~\hat{j} \right]\)
Sustituyendo:
\({{\vec{F}}_{1T}}~=9~\times ~{{10}^{9}}\cdot \times ~{{10}^{-6}}~\left[ \left( \frac{3\times ~{{10}^{-6}}~}{{{\left( 6\text{ }\!\!~\!\!\text{ }\times ~{{10}^{-2}} \right)}^{2}}}-\frac{~5\text{ }\!\!~\!\!\text{ }\times ~{{10}^{-6}}~}{{{\left( 6\text{ }\!\!~\!\!\text{ }\times ~{{10}^{-2}} \right)}^{2}}}~\cos 60~ \right)~\hat{i}-\frac{\text{ }\!\!~\!\!\text{ }5\text{ }\!\!~\!\!\text{ }\times ~{{10}^{-6}}~}{{{\left( 6\text{ }\!\!~\!\!\text{ }\times ~{{10}^{-2}} \right)}^{2}}}~\text{sen}60~\hat{j} \right]\)
\({{\vec{F}}_{1T}}~=\left[ 2.5~\hat{i}-~21.65~j \right]~N\)
Autora
 Escrito por Lismarihen Larreal para la Edición #103 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.
Escrito por Lismarihen Larreal para la Edición #103 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.