Constituyen cocientes entre los lados de un triángulo rectángulo, a título de razones trigonométricas, y se calculan en referencia a alguno de los dos ángulos agudos interiores de la figura, a lo que dependen sus valores independientemente del tamaño del triángulo.
Comúnmente, los ángulos se denotan mediante las letras minúsculas del alfabeto griego, como α (alfa), β (beta), γ (gamma), etc. Por su pate, el seno, el coseno y la tangente se abrevian como sen, cos y tan, respectivamente. Dado que siempre hay que hacer referencia al ángulo al que pertenecen, es correcto escribir “sen α”, “cos α” y “tan α”, que se leen como “seno de α”, “coseno de α” y “tangente de α”.
Fórmula para calcular las razones trigonométricas básicas de un ángulo agudo
Las tres razones trigonométricas son llamadas razones básicas. Para calcularlas se dispone de un triángulo rectángulo, que consta de dos lados “a” y “b”, llamados catetos, y un lado “c”, que siempre es más largo que estos, llamado hipotenusa.
Los catetos forman entre sí un ángulo recto, y entre la hipotenusa y los catetos se forman ángulos agudos, denotados como α y β, como se muestra en la siguiente figura:
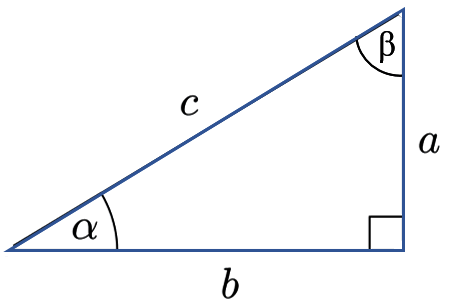
Mediante esta notación, las razones trigonométricas básicas del ángulo α se determinan del siguiente modo:
• \(sen~\alpha =\frac{{cateto~opuesto}}{{hipotenusa}}=~\frac{a}{c}\)
• \(cos~\alpha =\frac{{cateto~adyacente}}{{hipotenusa}}=~\frac{b}{c}\)
• \(tan~\alpha =\frac{{cateto~opuesto}}{{cateto~adyacente}}=~\frac{a}{b}\)
El término “cateto opuesto” hace referencia al cateto que está enfrente al ángulo α, es decir, el lado que no forma parte del ángulo. Mientras que el “cateto adyacente”, es uno de los lados que conforma el ángulo, y de allí viene el nombre de “adyacente”.
Nótese también que el cateto opuesto a α es adyacente a β, por lo que los valores del seno y el coseno de β, se intercambian con los de α. Esto significa que el sen β es cos α, y cos β es sen α.
Con esto en mente, las razones trigonométricas de β son:
• \(sen~\beta =\frac{{cateto~opuesto}}{{hipotenusa}}=~\frac{b}{c}\)
• \(cos~\beta =\frac{{cateto~adyacente}}{{hipotenusa}}=~\frac{a}{c}\)
• \(tan~\beta =\frac{{cateto~opuesto}}{{cateto~adyacente}}=~\frac{b}{a}\)
Las razones trigonométricas del ángulo agudo siempre son positivas, por ser cocientes entre longitudes, aunque el concepto se puede ampliar fácilmente para ángulos mayores a 90º.
Una característica importante, tanto del seno como del coseno de un ángulo agudo, es que su valor siempre es menor que 1. Y ello se debe a que la hipotenusa siempre tiene una mayor longitud que los catetos.
En cambio, la tangente del ángulo agudo puede ser mayor que 1, si el cateto opuesto al ángulo es más grande que el cateto adyacente. Y es exactamente igual a 1 solo cuando los catetos miden igual, pero esto solo ocurre cuando el ángulo en cuestión mide 45º.
Cosecante, la secante y la cotangente de un ángulo
Las razones trigonométricas inversas o recíprocas al seno, coseno y tangente reciben los nombres de cosecante, secante y cotangente.
Para el ángulo α, estas tres razones son:
• \(cosec~\alpha =\frac{{hipotenusa}}{{cateto~opuesto}}=~\frac{c}{a}\)
• \(sec~\alpha =\frac{{hipotenusa}}{{cateto~adyacente}}=~\frac{c}{b}\)
• \(cot~\alpha =\frac{{cateto~adyacente}}{{cateto~opuesto}}=~\frac{b}{a}\)
Conociendo las razones básicas, determinar estas otras es muy simple, pues solo basta con calcular la inversa.
A partir de esto, es posible darse cuenta de que la cosecante y la secante del ángulo agudo son mayores que 1, puesto que la hipotenusa siempre es más larga que los catetos. Además, cot α = tan β
Ejemplos aplicados de las razones trigonométricas
Tienen muchas aplicaciones, por ejemplo, sirven para resolver triángulos, es decir, hallar las longitudes de sus lados. Es posible establecer triángulos para determinar grandes alturas y distancias cuya medida directa pudiera ser engorrosa, o definitivamente inaccesible, como las que hay entre objetos astronómicos.
En física, las razones trigonométricas son necesarias para descomponer fuerzas, velocidades, aceleraciones y otros vectores, en sus componentes cartesianas. De esta manera se puede operar fácilmente con ellos, para hallar vectores resultantes, así como diferencias y productos entre vectores.
Magnitudes importantes como el trabajo que realiza una fuerza, están directamente relacionadas con el coseno del ángulo entre los vectores fuerza y desplazamiento, mientras que otras como el torque, se relacionan con el seno del ángulo entre la fuerza y la posición de su punto de aplicación respecto al eje de giro.
Ejercicio para probar los saberes
La distancia entre los puntos A y B de la siguiente figura es de 8 metros, y el ángulo de elevación, entre el punto A y el extremo superior del mástil de la bandera es 30º. La altura h del mástil se determina fácilmente a través de la tangente de 30º, que es el cociente entre la altura h y la distancia AB = 8 m:
\(\tan 30{}^\text{o}=~\frac{h}{{8~m}}\)
Por lo tanto:
\(h=8m\times \tan 30{}^\text{o}\)
El valor de tan 30º es 0.577, redondeado con 3 decimales y se halla fácilmente con una calculadora científica, por lo tanto, la altura buscada es:
\(h=8m\times 0.577=4.62~m\)

