En física el trabajo mecánico (\(W\)), es una cantidad física escalar, que relaciona la fuerza con el desplazamiento. Para definirlo consideremos la siguiente situación: un bloque se encuentra sobre una superficie horizontal como la mostrada en la figura, si aplicamos sobre él una fuerza \(F\) y como consecuencia de ella el bloque experimenta un desplazamiento \(d\) desde el punto inicial A hasta el punto final B, entonces se dice que la fuerza \(F\) ha realizado un trabajo mecánico sobre el cuerpo.
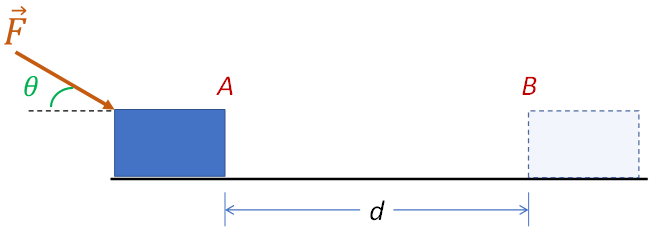
Donde \(\theta \) representa el menor ángulo entre \(F\) y \(d\), así si:
\(0~\le ~\theta ~\left\langle 90{}^\circ ~~\Rightarrow W~ \right\rangle 0\)
\(\theta =90{}^\circ ~~\Rightarrow W=0\)
\(90{}^\circ ~<~\theta ~\le 180{}^\circ ~~\Rightarrow W~<0\)
La unidad del trabajo es fuerza por distancia, es decir, Newton • metro (N • m). Esta unidad en el sistema internacional (SI) recibe el nombre de Joule (J).
Si temernos ahora una fuerza variable y deseamos conocer el trabajo que esta fuerza realiza para mover un cuerpo a lo largo de un desplazamiento dado, se divide el desplazamiento total en pequeños desplazamientos infinitesimales \(dl\), en donde puede considerarse que la fuerza es constante y el desplazamiento recto, se calcula el trabajo para cada desplazamiento infinitesimal que realiza la fuerza, y el trabajo total será igual a la suma de cada una de esas contribuciones.
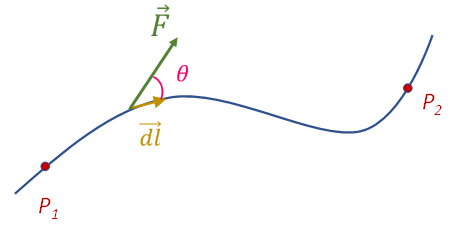
Así, el trabajo mecánico realizado por una fuerza variable para mover un cuerpo desde un punto inicial \({{P}_{1}}\) hasta un punto final \({{P}_{2}}\) en un trayecto, se traduce en:
\({{W}_{T}}=~\underset{{{P}_{1}}}{\overset{{{P}_{2}}}{\mathop \int }}\,F~dl\cos \theta =~\underset{{{P}_{1}}}{\overset{{{P}_{2}}}{\mathop \int }}\,\vec{F}\cdot \overrightarrow{dl}\)
Existe una relación entre el trabajo y la energía, puesto que el trabajo realizado por una fuerza, se relaciona con los cambios de energía que experimenta el cuerpo. Se dice que un cuerpo tiene energía si es capaz de realizar un trabajo, es decir, “el trabajo es una transferencia de energía”. Dependiendo del signo del trabajo realizado por un agente externo sobre un sistema, se puede saber si el sistema ha experimentado una pérdida o una ganancia de energía, así, si \(W<0\) se dice que el sistema ha perdido energía, mientras si \(W>0\) se dice que el sistema ha ganado energía.
Diferencia entre las fuerzas conservativas y no conservativas
Desde el punto de vista de la energía no todas las fuerzas tienen el mismo comportamiento, ya que el trabajo mecánico que ellas realizan sobre el sistema o cuerpo, puede depender o no de la trayectoria seguida por el cuerpo durante su desplazamiento. Esta relación entre el trabajo realizado por una fuerza y la trayectoria de su desplazamiento, permite clasificar las fuerzas en dos tipos: fuerzas conservativas y fuerzas no conservativas.
• Fuerzas conservativas: son aquellas fuerzas que conservan la energía del sistema y cumplen con las siguientes condiciones:
– El trabajo realizado puede expresarse como el negativo del cambio de energía potencial del sistema, es decir, W = -∆ U= -(Uf – Ui)).
– El trabajo realizado es reversible.
– El trabajo es independiente de la trayectoria, sólo depende de los puntos inicial y final.
– Si el punto inicial y final coinciden (trayectoria cerrada), el trabajo realizado es cero (nulo).
Las fuerzas que cumplen con estas condiciones son: la fuerza gravitatoria (el peso), la fuerza elástica (fuerza del resorte) y la fuerza eléctrica.
• Fuerzas no conservativas: son aquellas que disipan la energía del sistema, como la fuerza de fricción, y cuyo trabajo depende de la trayectoria seguida por el cuerpo, es decir, no cumplen con las condiciones antes mencionadas de fuerzas conservativas.
El trabajo W hecho por una fuerza variable que actúa sobre un objeto y que lo desplaza desde la posición A\(~\) hasta la posición B, es la integral del producto escalar entre la fuerza \(\vec{F}\) y un desplazamiento infinitesimal \(\overrightarrow{dr}\) sobre el camino C, que conecta el punto A con el B: \(W=\mathop{\int }_{A,~~~C}^{B}\vec{F}\cdot d\vec{r}\)
Ejemplos de fuerzas variables
• La fuerza aplicada para mover un mueble, la cual va aumentando hasta lograr su deslizamiento.
• La fuerza electrostática entre dos cargas puntuales, que depende del inverso del cuadrado de la separación entre las cargas
• La fuerza que un resorte ejerce sobre un objeto sujeto a él, la cual aumenta con el estiramiento y es opuesta al mismo.
Para simplificar, se supondrá un caso en el que la fuerza y el desplazamiento ocurren en una sola dirección, la del eje X. Por otra parte, si la fuerza varía con la posición “x” entonces el trabajo W realizado por la fuerza es equivalente al área bajo la gráfica F(x) versus x, desde \({{x}_{1}}~\)hasta \({{x}_{2}}\):
\(W=\mathop{\int }_{{{x}_{1}}}^{{{x}_{2}}}F\left( x \right)~dx\)
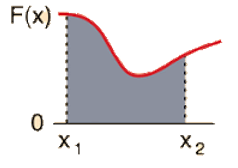
Recuérdese que solo la componente de la fuerza en la dirección del movimiento, es capaz de hacer trabajo sobre el objeto, esta es la componente tangencial de la fuerza.
Si la componente tangencial tiene el mismo sentido que el desplazamiento, el trabajo es positivo, si tiene sentido opuesto, es negativo. Por último, una fuerza perpendicular al desplazamiento no hace trabajo sobre el objeto.
Trabajo hecho para comprimir o estirar un resorte
Es sabido que, al comprimir un resorte, y luego ponerlo en contacto con un objeto, cuando el resorte se libera y se estira, es capaz de impulsar al cuerpo. Mientras más se trata de comprimir (o estirar) un resorte, más trabajo tiene que hacer el agente externo, y este trabajo queda almacenado en el resorte.
En tal caso, la ley de Hooke afirma que la magnitud de la fuerza que hay que aplicar es proporcional a la compresión o alargamiento del resorte:
\({{F}_{s}}=k\text{ }\!\!\Delta\!\!\text{ }x=k\left( x-{{x}_{o}} \right)\)
Donde “k” es la constante del resorte y “x” es la posición del extremo no fijo del resorte una vez que se comprimió o se estiró respecto a la posición de equilibrio xo (aquella posición en la cual el resorte no está estirado ni comprimido), la cual generalmente se toma como xo = 0, en cuyo caso:
\({{F}_{s}}=k\text{x}\)
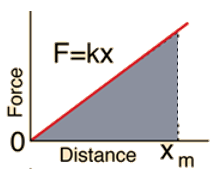
La gráfica de esta fuerza es una recta que pasa por el origen, así que para calcular el trabajo que hay que hacer para comprimir o estirar el resorte, basta con encontrar el área bajo la gráfica F versus x, entre los puntos x1 y x2 deseados.
En la siguiente figura se muestra la gráfica de F en función de x. Cuando el resorte se comprime o se estira desde x = 0 hasta x = xm, el trabajo necesario se calcula el área del triángulo sombreado:
\(W=\frac{1}{2}~base~\times altura=\frac{1}{2}x\cdot kx=\frac{1}{2}k{{x}^{2}}\)
Ejercicios a nivel práctico
1.- Supóngase que la gráfica de una fuerza horizontal, en función de la distancia recorrida es la siguiente:
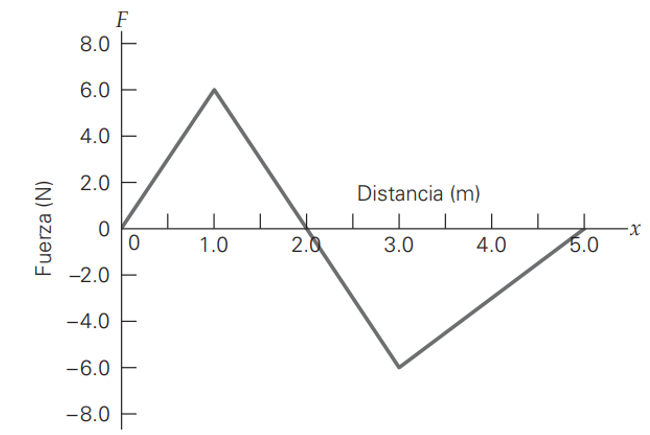
Calcular el trabajo realizado sobre el objeto para moverlo:
a) Desde x = 0m hasta x = 2m
b) De x = 2m hasta x = 3m
c) Desde x = 3m hasta x = 5m
d) Partiendo de x = 0m hasta x = 5m
Respuestas
a) Se calcula el área del triángulo cuya base es 2m y altura es 6N:
\(W=\frac{1}{2}~base~\times altura=\frac{1}{2}\cdot 2m\cdot 6N=6~J\)
b) Nuevamente, se calcula el trabajo a través del área del triángulo, pero teniendo en cuenta en este caso que la fuerza es negativa, el signo negativo debe acompañar al resultado. Este signo indica que la fuerza ha cambiado de sentido y ahora se opone al desplazamiento, por lo tanto, el trabajo que efectúa es negativo:
\(W=\frac{1}{2}\cdot 1m\cdot \left( -6N \right)=-3~J\)
c) Se procede como en el inciso anterior:
\(W=\frac{1}{2}\cdot 2m\cdot \left( -6N \right)=-6~J\)
d) El trabajo hecho por la fuerza sobre el móvil, desde x=0 m hasta x = 5m, es la suma algebraica de los trabajos calculados previamente, este es el trabajo neto:
\({{W}_{n}}=6J-3J-6J=-3J\)
2.- Una persona transporta una carga con ayuda de un carrito, moviéndose sobre una superficie horizontal. Ella aplica una fuerza cuya magnitud va en aumento, inclinada un ángulo θ variable, con respecto a la horizontal. La fuerza, en newton, tiene la forma:
\(F\left( x \right)=50x\)
Y el coseno del ángulo variable es:
\(\cos \theta =0.8-0.06x\)
¿Cuánto trabajo hace la persona al mover el carrito desde x = 5 m hasta x = 10m? Supóngase que el carrito no tiene rozamiento.
Respuesta
Se usa:
\(W=\mathop{\int }_{{{x}_{1}}}^{{{x}_{2}}}Fcos\theta dx\)
Por lo tanto:
\(W=\mathop{\int }_{5}^{10}50x\cdot \left( 0.8-0.06x \right)dx=\mathop{\int }_{5}^{10}\left( 40x-3{{x}^{2}} \right)dx=\mathop{\int }_{5}^{10}40xdx-\mathop{\int }_{5}^{10}3{{x}^{2}}dx\)
\(W=\left. 40\left( \frac{{{x}^{2}}}{2} \right) \right|_{5}^{10}-3\left. \left( \frac{{{x}^{3}}}{3} \right) \right|_{5}^{10}=20\left( ~{{10}^{2}}-{{5}^{2}} \right)-\left( ~{{10}^{3}}-{{5}^{3}} \right)=625~J\)
Referencias bibliográficas
• Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).• Wilson, J. 2007. Física. Prentice Hall.
Autora
 Escrito por Lismarihen Larreal para la Edición #103 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.
Escrito por Lismarihen Larreal para la Edición #103 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.