La velocidad es una cantidad física vectorial que se utiliza para caracterizar el movimiento de los cuerpos y partículas, permitiendo medir cómo se mueven y hacia dónde lo hacen, y establecer cuán rápido o lento es su movimiento con respecto a otro.
La velocidad puede definirse como el cociente entre el desplazamiento realizado por un cuerpo/partícula y el tiempo empleado para dicho desplazamiento. En otras palabras, la velocidad es el cambio de posición que experimenta un cuerpo/partícula dividido entre el tiempo empleado para realizarlo, comprendiendo así la tasa de cambio de la posición con respecto al tiempo. Puesto que el cambio de la posición (desplazamiento) puede ser finito o infinitesimal, existen dos tipos de velocidades: la velocidad media y la velocidad instantánea.
• Velocidad media (\({{V}_{m}})\): es la relación entre el desplazamiento realizado por cuerpo o partícula en un intervalo de tiempo dado. Matemáticamente se define como:
\(\overrightarrow{{{V}_{m}}}~=~\frac{\overrightarrow{\Delta x}}{\Delta t}\)
Su dimensión es longitud entre tiempo, por lo tanto, en el sistema internacional (SI) se expresa en \({}^{m}\!\!\diagup\!\!{}_{s}\;\).
De la expresión anterior se puede deducir que la velocidad media y el desplazamiento siempre tienen la misma dirección y sentido, puesto que, el intervalo de tiempo \(\Delta t\) siempre es positivo.
Ejemplo: En la figura 1 se muestra el recorrido que realiza una partícula desde el punto O (origen del sistema de referencia) hasta el punto B. Determine la velocidad media en los tramos OA y AB.
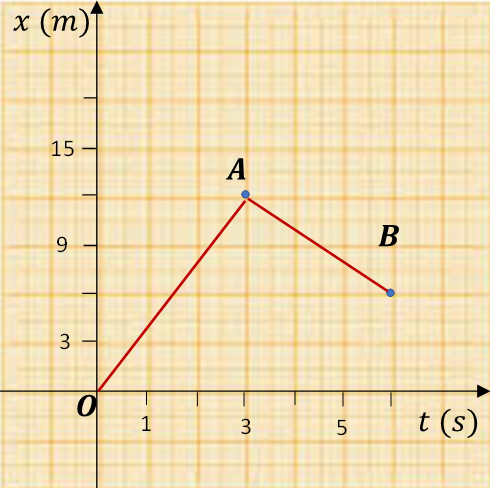
Figura 1. Grafica de la posición de una partícula en función del tiempo.
Para calcular la velocidad media en cada tramo, debemos determinar a partir de la gráfica, la posición y el tiempo para cada punto. Así:
\({{x}_{O}}=0~m,~~{{t}_{O}}=0~s~~~;~~{{x}_{A}}=12~m,~~{{t}_{A}}=3~s~~~;~{{x}_{B}}=6~m,~~{{t}_{B}}=6~s~~~\)
Para el tramo OA:
\(\overrightarrow{V{{m}_{OA}}}~=~\frac{\overrightarrow{\Delta {{x}_{OA}}}}{\Delta {{t}_{OA}}}=~\frac{{{x}_{A}}-~{{x}_{O}}}{{{t}_{A}}-~{{t}_{O}}}=~\frac{12-0}{3-0}\)
\(\overrightarrow{V{{m}_{OA}}}~=4~{}^{m}\!\!\diagup\!\!{}_{s}\;~\)
Para el tramo AB:
\(\overrightarrow{V{{m}_{AB}}}~=~\frac{\overrightarrow{\Delta {{x}_{AB}}}}{\Delta {{t}_{AB}}}=~\frac{{{x}_{B}}-~{{x}_{A}}}{{{t}_{B}}-~{{t}_{A}}}=~\frac{6-12}{6-3}\)
\(\overrightarrow{V{{m}_{OA}}}~=-2~{}^{m}\!\!\diagup\!\!{}_{s}\;~\)
• Velocidad instantánea (\(V)\): si se realiza un desplazamiento en un intervalo de tiempo infinitesimal (\(lim\Delta t~\to 0\)), es decir, cuando el instante de tiempo inicial y final tienden a ser iguales, en este caso la velocidad se conoce como velocidad instantánea.
Matemáticamente se defina la velocidad instantánea como:
\(~V~=~\underset{\Delta t~\to 0}{\mathop{\lim }}\,\frac{\Delta x}{\Delta t}=~\frac{dx}{dt}\)
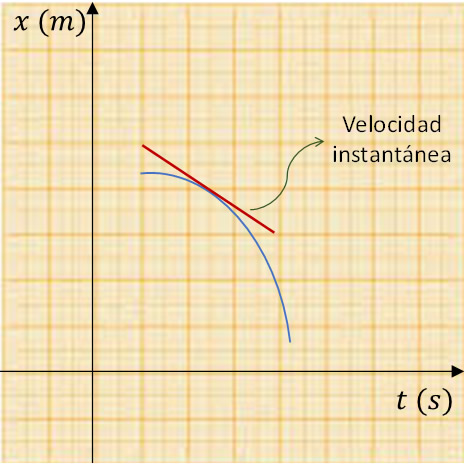
La velocidad instantánea es la derivada del desplazamiento con respecto al tiempo, por lo que la velocidad es siempre tangente a la trayectoria descrita por el cuerpo o partícula. Gráficamente, la velocidad instantánea representa la pendiente de la tangente en la gráfica de posición vs. tiempo, como se muestra en la figura.
Ejemplo: considere un cuerpo cuyo desplazamiento está dado por la siguiente ecuación
\({{x}_{\left( t \right)}}=5{{t}^{2}}-2t+3\)
Donde \(x\) está expresada en metros y \(t\) en segundos. Determine la velocidad a los 3 segundos.
Para determinar la velocidad a los 3 segundos, utilizamos la definición de velocidad instantánea:
\(V~=~\frac{dx}{dt}\)
Al derivar con respecto al tiempo la ecuación de posición tenemos:
\(V~=~\frac{dx}{dt}=~10t-2\)
La expresión anterior, nos permite determinar la velocidad instantánea de la partícula para cualquier tiempo. Evaluando la expresión en \(t=3~s\), tenemos:
\(V=28~{}^{m}\!\!\diagup\!\!{}_{s}\;\)
En ocasiones suele confundirse velocidad con rapidez. La rapidez (\(r\)) es una cantidad física escalar que se define como la distancia recorrida en un intervalo de tiempo determinado, es decir, la longitud de la trayectoria entre el tiempo. Se expresa como:
\(r=~\frac{distancia~recorrida}{tiempo}~\)
Cuando se realiza un movimiento rectilíneo en una misma dirección y sentido, la rapidez coincide con la magnitud de la velocidad, es por esta razón que se presenta la confusión entre ambos términos.
Diferencias entre rapidez y velocidad
1. La velocidad es una cantidad vectorial (posee magnitud, dirección y sentido) mientras que la rapidez es una cantidad escalar.
2. La velocidad depende de la posición inicial y final del cuerpo o partícula, es decir, de su desplazamiento; mientras que la rapidez depende de la trayectoria recorrida (distancia recorrida).
Ejemplo: en una carrera de atletismo de 400 metros el atleta A completa la prueba en 47,6 s. Determine su rapidez y velocidad media.
Para calcular la rapidez, tenemos que
\(r=~\frac{distancia~recorrida}{tiempo}=~\frac{400~m}{47,6~s}~=8,40~{}^{m}\!\!\diagup\!\!{}_{s}\;\)
En cuanto a su velocidad media, por definición, es igual al vector desplazamiento entre el tiempo, es decir:
\(\overrightarrow{{{V}_{m}}}~=~\frac{\overrightarrow{\Delta x}}{\Delta t}=~\frac{\overrightarrow{{{x}_{f}}}-~\overrightarrow{{{x}_{i}}}}{\Delta t}\)
El atleta inició y finalizó su recorrido de 400 m en el mismo punto, por lo que su desplazamiento fue nulo, por lo tanto, su velocidad media es cero.
\(\overrightarrow{{{V}_{m}}}~=0\)
Autora
 Escrito por Lismarihen Larreal para la Edición #104 de Enciclopedia Asigna, en 10/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.
Escrito por Lismarihen Larreal para la Edición #104 de Enciclopedia Asigna, en 10/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.